A Simple Backgammon Lesson
by
Edward
D. Collins

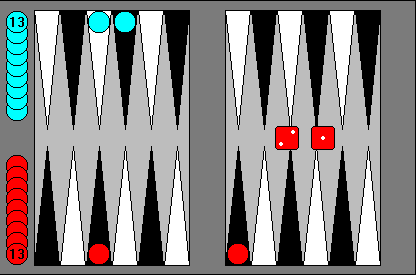
In the above position both sides each have two men left to bear off, having already borne-off 13 men. It's Red's turn to move and he has just rolled a 2-1. As Blue will almost certainly be able to bear off both his checkers in two moves, Red must give himself the best chance to bear off both of his checkers on his following move. With this in mind, what is his proper play now?
Before we answer this question let's take a moment and review all 36 possible ways that a pair of dice can be thrown. This graphic below that I put together illustrates this nicely. |

I've colored each of the two dice differently, to help show that a roll of "2-1" is actually a different roll than a "1-2." As far as backgammon is concerned, it does amount to the same thing but it is indeed a different roll. As the above table shows, there is only one way, for example, to roll boxcars (double-sixes). You MUST roll a 6 with the first die, and then you MUST roll a 6 with the second die. This means that the chances of rolling double sixes are 1/6 x 1/6 or 1/36, otherwise known as 35 to 1 against. In fact, the chances of rolling ANY of the above specific dice rolls are also 35 to 1. Playing a game and you need to roll a red 5 and a white 4? The odds are 35 to 1 against you doing so. But note that there are two ways to roll a 2 and a 1 combination, for example. You can roll a "2-1" or a "1-2." Your first dice roll is not limited to just a certain number, like with the boxcars. On the first roll you can roll a 2 OR a 1. However, once you've rolled this, the second die that you throw must come up with either a 1 or a 2 depending on what you rolled with the first die. So then, the chances of rolling a 2 and a 1 (or a 1 and a 2) are 2/6 x 1/6 or 2/36 which reduces to 1/18 or only 17 to 1 against - twice as likely! Need to roll a double, any double to win a game? By glancing at the above table you can easily see that there are just 6 ways to do so. A 1-1, which can only be rolled one way, as well as a 2-2, 3-3, 4-4, 5-5, and 6-6. Six possibilities from a total of 36. 6/36 reduces to 1/6 or 5 to 1 against you rolling that double. Need to roll anything but a 1? Without glancing at the table, simple arithmetic can give us the answer: Five chances on the first die multiplied by five chances on the second. 5/36 x 5/36 or 25/36. 25 rolls will give us a combination which does not include a 1 as the above table will confirm. Now, back to our problem. If the player chooses the first choice, he will be left with a checker on both his three-point and his four-point. The cells marked in blue in this table below show the rolls that will bear off both of these men on the next turn. |

If we add these up we see that there are 17 of them. 17 rolls our of 36 - slightly less than a 50 percent chance. However, if Red decides to use the second option and move the checker on his seven-point with the 1 and the checker on his three-point with the 2, he will be left with checkers on his one-point and six-point. This next table marks the rolls which will bear off those checkers on the next roll: |

Add these up. Upon doing so, you'll see that there are just 15 rolls this time. The number is reduced because Red MUST roll a 6, unless he rolls doubles. (But not double-ones.) So leaving men on the one-point and the six-point is slightly less desirable than leaving them on the three-point and four-point! But let's now look at the third option. This produces a position with a checker remaining on the two-point and the five-point. Once again, this next table highlights the cells which will bear off those checkers on the next move from that position: |

What have we here? 19 cells are marked?? That's right, folks. Leaving checkers on your two-point and your five-point in this example is the best way to go. You give yourself more chances of bearing off both your checkers on the next roll if you do so. Here we have a better than 50 - 50 chance! Happy playing! Note that in the first paragraph above, I said that Blue would almost certainly bear off both of his checkers in two moves. But there is one scenario in which this doesn't happen -- if he rolls a 1 - 2 (or 2 - 1) combination twice! And what are the chances of that happening? Let's figure it out: He has but two chances out of 36 on his first roll and then assuming he rolls this, he has just another two chances out of his 36 on his second roll. 2/36 x 2/36 = 4/1,296 which reduces to just one chance in 324! Talk about a longshot! |